Optimal Classification Trees¶

Classification trees are among the most popular and inherently interpretable machine learning models and are used routinely in applications ranging from revenue management and medicine to bioinformatics. In these settings, it is crucial to leverage the full potential of available data to obtain the best possible, i.e., optimal, classification tree. We say that a classification tree is optimal if there exists a mathematical proof that no other tree yields a lower misclassification rate in the population used for training the method. StrongTree is a Mixed-Integer Optimization (MIO) based formulation for learning optimal classification trees of a given depth. StrongTree significantly improves upon traditional heuristic approaches in terms of performance, is much faster than other MIO-based alternatives, and can handle real-valued covariates, unlike existing MIO-based methods. See the corresponding paper for a complete treatment of StrongTree (Aghaei et al., 2021).

Choosing an Objective to Optimize¶

FlowOCT and BendersOCT provide three options for the objective function through the obj_mode parameter: "acc", "balance", and "custom".

When obj_mode="acc", the classifier will attempt to maximize the classification accuracy.
When obj_mode="balance", it will maximize the balanced accuracy, which averages the accuracy across classes.
When obj_mode="custom", it allows the user to provide custom weights for each sample during the fit process.

The balanced accuracy can be helpful in the case of imbalanced datasets. A dataset is imbalanced when the class distribution is not uniform, i.e., when the number of data points in each class varies significantly between classes. For an imbalanced dataset, predicting the majority class results in high accuracy. Thus decision trees that maximize prediction accuracy without accounting for the imbalanced nature of the data perform poorly on the minority class. Imbalanced datasets occur in many important domains, e.g., in a problem such as suicide prevention, there are a very small number of suicide instances.

The custom weights option provides even more flexibility in handling imbalanced datasets or scenarios where misclassification costs vary across samples. By specifying obj_mode="custom" and providing a weight for each sample when calling the fit method, users can control the importance of each sample in the optimization process. This can be particularly useful when certain samples are more important or costly to misclassify than others.

For example, to use custom weights:

weights = np.ones(len(y))
weights[y == minority_class] = 10  # Give more weight to minority class samples

clf = FlowOCT(obj_mode="custom")
clf.fit(X, y, weights=weights)

This approach allows for fine-grained control over the optimization process, enabling the classifier to focus on correctly predicting specific samples or classes that are deemed more important for the given problem.

Optimality¶

The FlowOCT and BendersOCT classes provide an argument, time_limit for limiting the amount of time the solver will spend finding the optimal decision tree. The default time limit is 60 seconds and once the specified solving time has elapsed, the classifier will return the resulting decision tree and report the optimality gap, which is an indicator of the quality of the solution. The optimality gap is an indicator of the quality of the solution, i.e., how far our solution is from the optimal solution (in the case of optimality, the gap is zero). For larger problems it may be necessary to increase the time limit to allow the classifier to find a high-quality solution.

Speeding up Computation: Benders’ Decomposition¶

ODTlearn offers a novel Benders’ decomposition-based algorithm for solving the problem of learning optimal classification trees. This algorithm is implemented in the BendersOCT class. For the majority of use-cases we recommend the Benders’ decomposition-based algorithm because it is significantly faster than the direct approach implemented in FlowOCT.

Regularization¶

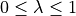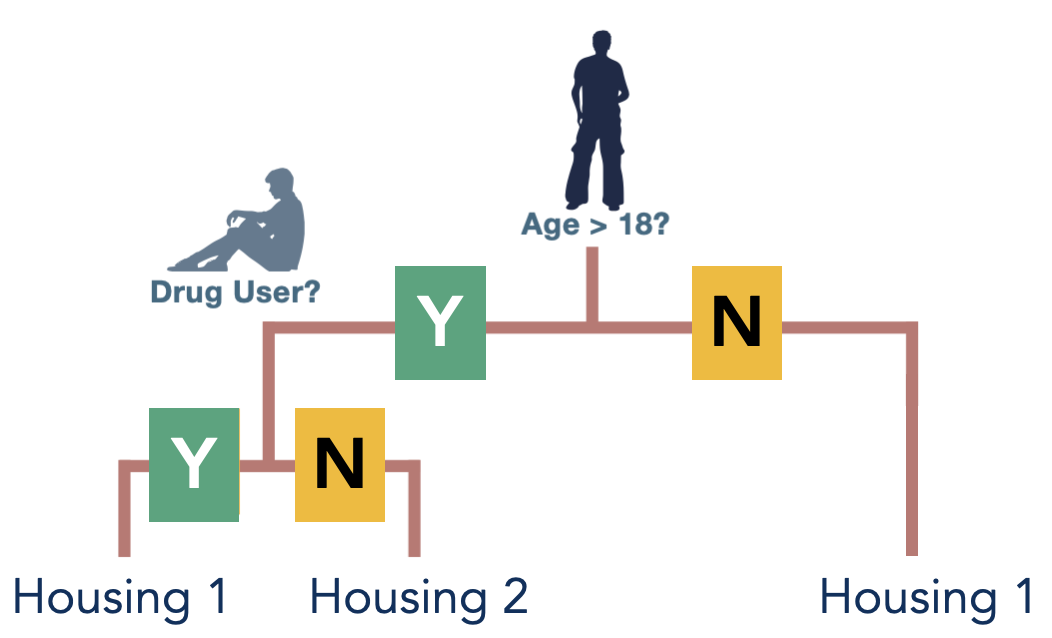
To avoid overfitting on the training data, a regularization term ( $0 \leq \lambda \leq 1$ ) can be specified in FlowOCT and BendersOCT. This regularization term penalizes the number of branching nodes in the decision tree. A higher value of $\lambda$ results in a sparser decision tree, i.e., a decision tree where the distance of its leaf nodes from the root node is not the same. Figure 2 shows an example of an imbalanced decision tree. You can set the value of $\lambda$ via parameter _lambda in FlowOCT and BendersOCT.

Handling Integer Features¶

StrongTree requires all the input features to be binary, i.e., all the elements of the feature matrix 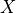$X$ should be either 0 or 1. However, this formulation can also be applied to datasets involving categorical, integer, or continuous features by first preprocessing the data.

ODTlearn provides a function called binarize for handling the binarization step. When provided a data frame with categorical, integer, or continuous columns, the function outputs a binarized data frame. The binarization process works as follows:

For categorical features: It encodes each level as a one-hot vector, i.e., for each level of the feature, it creates a new binary column with a value of one if and only if the original column has the corresponding level.
For integer features: It creates multiple binary columns, where each new column has a value of one if and only if the main column has the corresponding value or any value smaller than it.
For continuous features: It first discretizes the values into a specified number of bins (default is 4), and then treats these bins as ordinal integer features, applying the same process as for integer features.

Here’s an example of how to use the binarize function:

from odtlearn.utils.binarize import binarize

binarized_df = binarize(
    df, 
    categorical_cols=["sex", "race"], 
    integer_cols=["num_child"], 
    real_cols=["age"],
    n_bins=5  # Number of bins for continuous features
)

This preprocessing step allows FlowOCT and BendersOCT to handle a wide range of feature types while maintaining the binary input requirement of the StrongTree formulation. The binarization of continuous features enables the model to find optimal split points within the specified number of bins, providing a balance between granularity and computational efficiency.

References¶

Aghaei, S., Gómez, A., & Vayanos, P. (2021). Strong optimal classification trees. arXiv preprint arXiv:2103.15965. https://arxiv.org/abs/2103.15965