[1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from odtlearn.flow_oct import FlowOCT, BendersOCT
from odtlearn.utils.binarize import Binarizer
FlowOCT Examples¶
Example 0: Binarization¶
The following example shows how to binarize a dataset with categorical, integer, and continuous features using the built-in Binarizer class. This class follows the scikit-learn fit-transform paradigm, making it easy to integrate into your preprocessing pipeline.
[2]:
number_of_child_list = [1, 2, 4, 3, 1, 2, 4, 3, 2, 1]
age_list = [10, 20, 40, 30, 10, 20, 40, 30, 20, 10]
race_list = [
"Black",
"White",
"Hispanic",
"Black",
"White",
"Black",
"White",
"Hispanic",
"Black",
"White",
]
sex_list = ["M", "F", "M", "M", "F", "M", "F", "M", "M", "F"]
income_list = [50000, 75000, 100000, 60000, 80000, 55000, 90000, 70000, 85000, 65000]
df = pd.DataFrame(
list(zip(sex_list, race_list, number_of_child_list, age_list, income_list)),
columns=["sex", "race", "num_child", "age", "income"],
)
print(df)
sex race num_child age income
0 M Black 1 10 50000
1 F White 2 20 75000
2 M Hispanic 4 40 100000
3 M Black 3 30 60000
4 F White 1 10 80000
5 M Black 2 20 55000
6 F White 4 40 90000
7 M Hispanic 3 30 70000
8 M Black 2 20 85000
9 F White 1 10 65000
[3]:
binarizer = Binarizer(
categorical_cols=["sex", "race"],
integer_cols=["num_child", "age"],
real_cols=["income"],
n_bins=5 # Number of bins for continuous features
)
# Fit and transform the data
df_enc = binarizer.fit_transform(df)
print(df_enc)
sex_M race_Black race_Hispanic race_White num_child_1 num_child_2 \
0 1.0 1.0 0.0 0.0 1.0 1.0
1 0.0 0.0 0.0 1.0 0.0 1.0
2 1.0 0.0 1.0 0.0 0.0 0.0
3 1.0 1.0 0.0 0.0 0.0 0.0
4 0.0 0.0 0.0 1.0 1.0 1.0
5 1.0 1.0 0.0 0.0 0.0 1.0
6 0.0 0.0 0.0 1.0 0.0 0.0
7 1.0 0.0 1.0 0.0 0.0 0.0
8 1.0 1.0 0.0 0.0 0.0 1.0
9 0.0 0.0 0.0 1.0 1.0 1.0
num_child_3 num_child_4 age_10 age_20 age_30 age_40 income_0 \
0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1 1.0 1.0 0.0 1.0 1.0 1.0 0.0
2 0.0 1.0 0.0 0.0 0.0 1.0 0.0
3 1.0 1.0 0.0 0.0 1.0 1.0 0.0
4 1.0 1.0 1.0 1.0 1.0 1.0 0.0
5 1.0 1.0 0.0 1.0 1.0 1.0 1.0
6 0.0 1.0 0.0 0.0 0.0 1.0 0.0
7 1.0 1.0 0.0 0.0 1.0 1.0 0.0
8 1.0 1.0 0.0 1.0 1.0 1.0 0.0
9 1.0 1.0 1.0 1.0 1.0 1.0 0.0
income_1 income_2 income_3 income_4
0 1.0 1.0 1.0 1.0
1 0.0 1.0 1.0 1.0
2 0.0 0.0 0.0 1.0
3 1.0 1.0 1.0 1.0
4 0.0 0.0 1.0 1.0
5 1.0 1.0 1.0 1.0
6 0.0 0.0 0.0 1.0
7 0.0 1.0 1.0 1.0
8 0.0 0.0 1.0 1.0
9 1.0 1.0 1.0 1.0
The Binarizer class follows the scikit-learn fit-transform paradigm:
We initialize the Binarizer with our desired parameters, specifying which columns are categorical, integer, and real-valued. We call the fit_transform method, which first fits the binarizer to our data (learning the necessary encoding schemes) and then transforms the data using those learned encodings.
The resulting df_enc DataFrame contains the binarized version of our original data:
Categorical columns (sex, race) are one-hot encoded. Integer columns (num_child, age) are binary encoded, where each column represents “greater than or equal to” a certain value. The continuous column (income) is first discretized into 5 bins, then binary encoded similar to the integer columns.
[4]:
print(df_enc.columns)
Index(['sex_M', 'race_Black', 'race_Hispanic', 'race_White', 'num_child_1',
'num_child_2', 'num_child_3', 'num_child_4', 'age_10', 'age_20',
'age_30', 'age_40', 'income_0', 'income_1', 'income_2', 'income_3',
'income_4'],
dtype='object')
This binarized data is now ready to be used with any of the models in ODTlearn, which require binary input features. If you need to transform new data using the same encoding scheme, you can use the transform method of the fitted binarizer:
[5]:
new_data = pd.DataFrame({
"sex": ["F", "M"],
"race": ["Hispanic", "White"],
"num_child": [2, 3],
"age": [20, 30],
"income": [70000, 80000]
})
new_data_enc = binarizer.transform(new_data)
print(new_data_enc)
sex_M race_Black race_Hispanic race_White num_child_1 num_child_2 \
0 0.0 0.0 1.0 0.0 0.0 1.0
1 1.0 0.0 0.0 1.0 0.0 0.0
num_child_3 num_child_4 age_10 age_20 age_30 age_40 income_0 \
0 1.0 1.0 0.0 1.0 1.0 1.0 0
1 1.0 1.0 0.0 0.0 1.0 1.0 0
income_1 income_2 income_3 income_4
0 0 1.0 1.0 0
1 0 0.0 1.0 0
Note that for categorical features, if the new data contains categories not seen during fitting, the transform method will raise an error. In such cases, you might need to refit the binarizer on a dataset that includes all possible categories.
Example 1: Varying depth and _lambda¶
In this part, we study a simple example and investigate different parameter combinations to provide intuition on how they affect the structure of the tree.
First we generate the data for our example. The diagram within the code block shows the training dataset. Our dataset has two binary features (X1 and X2) and two class labels (+1 and -1).
[6]:
from odtlearn.datasets import flow_oct_example
"""
X2
| |
| |
1 + + | -
| |
|---------------|-------------
| |
0 - - - - | + + +
| - - - |
|______0________|_______1_______X1
"""
X, y = flow_oct_example()
Tree with depth = 1¶
In the following, we fit a classification tree of depth 1, i.e., a tree with a single branching node and two leaf nodes.
[7]:
stcl = FlowOCT(depth=1, solver="gurobi", time_limit=100)
stcl.store_search_progress_log = True
stcl.fit(X, y)
Set parameter Username
Academic license - for non-commercial use only - expires 2025-06-28
Set parameter TimeLimit to value 100
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 110 rows, 89 columns and 250 nonzeros
Model fingerprint: 0x5e9209d1
Variable types: 84 continuous, 5 integer (5 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [1e+00, 1e+00]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Presolve removed 102 rows and 82 columns
Presolve time: 0.00s
Presolved: 8 rows, 7 columns, 16 nonzeros
Variable types: 6 continuous, 1 integer (1 binary)
Found heuristic solution: objective 9.0000000
Root relaxation: objective 1.000000e+01, 2 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
* 0 0 0 10.0000000 10.00000 0.00% - 0s
Explored 1 nodes (2 simplex iterations) in 0.00 seconds (0.00 work units)
Thread count was 8 (of 8 available processors)
Solution count 2: 10 9
Optimal solution found (tolerance 1.00e-04)
Best objective 1.000000000000e+01, best bound 1.000000000000e+01, gap 0.0000%
User-callback calls 573, time in user-callback 0.00 sec
[7]:
FlowOCT(solver=gurobi,depth=1,time_limit=100,num_threads=None,verbose=False)
[8]:
predictions = stcl.predict(X)
print(f'Optimality gap is {stcl.optim_gap}')
print(f"In-sample accuracy is {np.sum(predictions==y)/y.shape[0]}")
Optimality gap is 0.0
In-sample accuracy is 0.7692307692307693
Users can access statistics from the optimization run such as optimality gap, number of nodes, number of constraints, etc. Directly as properties of the initialized class or through the _solver object. For example, one can access the optimality gap and the number of solutions after fitting the optimal decision tree through the optim_gap and num_solutions properties.
[9]:
print(f'Optimality gap is {stcl.optim_gap}')
print(f'Number of solutions {stcl.num_solutions}')
Optimality gap is 0.0
Number of solutions 2
As we can see above, we find the optimal tree and the in-sample accuracy is 76%.
ODTlearn provides two different ways of visualizing the structure of the tree. The first method prints the structure of the tree in the console:
[10]:
stcl.print_tree()
#########node 1
branch on X_0
#########node 2
leaf 0
#########node 3
leaf 1
The second method plots the structure of the tree using matplotlib:
[11]:
fig, ax = plt.subplots(figsize=(5, 5))
stcl.plot_tree(ax=ax)
plt.show()

We also provide a simple function allowing users to plot the search progress log over time. Note that you must set the attribute store_search_progress_log to True before calling the fit method to ensure that the bound information is stored.
[12]:
stcl_progress_log = FlowOCT(depth=1, solver="gurobi", time_limit=100)
stcl_progress_log.store_search_progress_log = True
stcl_progress_log.fit(X, y)
Set parameter Username
Academic license - for non-commercial use only - expires 2025-06-28
Set parameter TimeLimit to value 100
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 110 rows, 89 columns and 250 nonzeros
Model fingerprint: 0x5e9209d1
Variable types: 84 continuous, 5 integer (5 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [1e+00, 1e+00]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Presolve removed 102 rows and 82 columns
Presolve time: 0.00s
Presolved: 8 rows, 7 columns, 16 nonzeros
Variable types: 6 continuous, 1 integer (1 binary)
Found heuristic solution: objective 9.0000000
Root relaxation: objective 1.000000e+01, 2 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
* 0 0 0 10.0000000 10.00000 0.00% - 0s
Explored 1 nodes (2 simplex iterations) in 0.01 seconds (0.00 work units)
Thread count was 8 (of 8 available processors)
Solution count 2: 10 9
Optimal solution found (tolerance 1.00e-04)
Best objective 1.000000000000e+01, best bound 1.000000000000e+01, gap 0.0000%
User-callback calls 573, time in user-callback 0.00 sec
[12]:
FlowOCT(solver=gurobi,depth=1,time_limit=100,num_threads=None,verbose=False)
[13]:
stcl.plot_search_progress()
[13]:
<AxesSubplot:title={'center':'Search Progress'}, xlabel='Time (s)', ylabel='Objective Bound'>
Tree with depth = 2¶
Now we increase the depth of the tree to achieve higher accuracy.
[14]:
stcl = FlowOCT(depth=2, solver="gurobi")
stcl.fit(X, y)
Set parameter Username
Academic license - for non-commercial use only - expires 2025-06-28
Set parameter TimeLimit to value 60
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 274 rows, 209 columns and 642 nonzeros
Model fingerprint: 0x51470803
Variable types: 196 continuous, 13 integer (13 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [1e+00, 1e+00]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Found heuristic solution: objective -0.0000000
Presolve removed 250 rows and 187 columns
Presolve time: 0.00s
Presolved: 24 rows, 22 columns, 76 nonzeros
Found heuristic solution: objective 8.0000000
Variable types: 16 continuous, 6 integer (6 binary)
Root relaxation: objective 1.300000e+01, 14 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
* 0 0 0 13.0000000 13.00000 0.00% - 0s
Explored 1 nodes (14 simplex iterations) in 0.00 seconds (0.00 work units)
Thread count was 8 (of 8 available processors)
Solution count 3: 13 8 -0
Optimal solution found (tolerance 1.00e-04)
Best objective 1.300000000000e+01, best bound 1.300000000000e+01, gap 0.0000%
[14]:
FlowOCT(solver=gurobi,depth=2,time_limit=60,num_threads=None,verbose=False)
[15]:
predictions = stcl.predict(X)
print(f"In-sample accuracy is {np.sum(predictions==y)/y.shape[0]}")
In-sample accuracy is 1.0
As we can see, with depth 2, we can achieve 100% in-sample accuracy.
[16]:
fig, ax = plt.subplots(figsize=(10, 5))
stcl.plot_tree(ax=ax, fontsize=20)
plt.show()
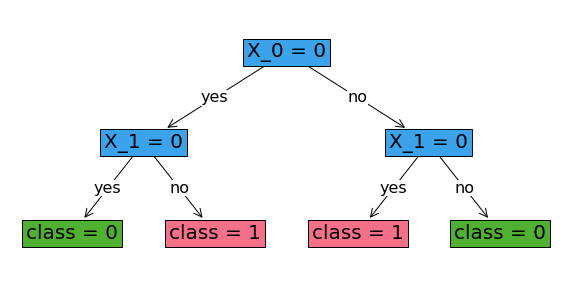
Tree with depth=2 and Positive _lambda¶
As we saw in the above example, with depth 2, we can fully classify the training data. However if we add a regularization term with a high enough value of _lambda, we can justify pruning one of the branching nodes to get a sparser tree. In the following, we observe that as we increase _lambda from 0 to 0.51, one of the branching nodes gets pruned and as a result, the in-sample accuracy drops to 92%.
[17]:
stcl = FlowOCT(solver="gurobi", depth=2, _lambda=0.51)
stcl.fit(X, y)
Set parameter Username
Academic license - for non-commercial use only - expires 2025-06-28
Set parameter TimeLimit to value 60
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 274 rows, 209 columns and 642 nonzeros
Model fingerprint: 0x3e3f455b
Variable types: 196 continuous, 13 integer (13 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [5e-01, 5e-01]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Found heuristic solution: objective -0.0000000
Presolve removed 250 rows and 187 columns
Presolve time: 0.00s
Presolved: 24 rows, 22 columns, 76 nonzeros
Found heuristic solution: objective 3.9200000
Variable types: 16 continuous, 6 integer (6 binary)
Root relaxation: objective 5.105000e+00, 14 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 5.10500 0 2 3.92000 5.10500 30.2% - 0s
H 0 0 4.8600000 5.10500 5.04% - 0s
Explored 1 nodes (14 simplex iterations) in 0.00 seconds (0.00 work units)
Thread count was 8 (of 8 available processors)
Solution count 3: 4.86 3.92 -0
Optimal solution found (tolerance 1.00e-04)
Best objective 4.860000000000e+00, best bound 4.860000000000e+00, gap 0.0000%
[17]:
FlowOCT(solver=gurobi,depth=2,time_limit=60,num_threads=None,verbose=False)
[18]:
predictions = stcl.predict(X)
print(f"In-sample accuracy is {np.sum(predictions==y)/y.shape[0]}")
In-sample accuracy is 0.9230769230769231
[19]:
fig, ax = plt.subplots(figsize=(10, 5))
stcl.plot_tree(ax=ax, fontsize=20)
plt.show()

Example 2: Different Objective Functions¶
In the following, we have a toy example with an imbalanced data, with the positive class being the minority class.
[20]:
'''
X2
| |
| |
1 + - - | -
| |
|---------------|--------------
| |
0 - - - + | - - -
| - - - - |
|______0________|_______1_______X1
'''
X = np.array([[0,0],[0,0],[0,0],[0,0],[0,0],[0,0],[0,0],[0,0],
[1,0],[1,0],[1,0],
[1,1],
[0,1],[0,1],[0,1]])
y = np.array([0,0,0,0,0,0,0,1,
0,0,0,
0,
1,0,0])
Tree with classification accuracy objective¶
[21]:
stcl_acc = FlowOCT(solver="gurobi", depth=2, obj_mode="acc")
stcl_acc.fit(X, y)
Set parameter Username
Academic license - for non-commercial use only - expires 2025-06-28
Set parameter TimeLimit to value 60
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 314 rows, 237 columns and 734 nonzeros
Model fingerprint: 0xa5b9a46b
Variable types: 224 continuous, 13 integer (13 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [1e+00, 1e+00]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Found heuristic solution: objective -0.0000000
Presolve removed 269 rows and 203 columns
Presolve time: 0.00s
Presolved: 45 rows, 34 columns, 134 nonzeros
Found heuristic solution: objective 13.0000000
Variable types: 27 continuous, 7 integer (7 binary)
Root relaxation: objective 1.400000e+01, 32 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 14.00000 0 1 13.00000 14.00000 7.69% - 0s
Cutting planes:
MIR: 1
Flow cover: 1
Explored 1 nodes (32 simplex iterations) in 0.00 seconds (0.00 work units)
Thread count was 8 (of 8 available processors)
Solution count 2: 13 -0
Optimal solution found (tolerance 1.00e-04)
Best objective 1.300000000000e+01, best bound 1.300000000000e+01, gap 0.0000%
[21]:
FlowOCT(solver=gurobi,depth=2,time_limit=60,num_threads=None,verbose=False)
[22]:
predictions = stcl_acc.predict(X)
print(f"In-sample accuracy is {np.sum(predictions==y)/y.shape[0]}")
In-sample accuracy is 0.8666666666666667
[23]:
stcl_acc.print_tree()
#########node 1
leaf 0
#########node 2
pruned
#########node 3
pruned
#########node 4
pruned
#########node 5
pruned
#########node 6
pruned
#########node 7
pruned
[24]:
fig, ax = plt.subplots(figsize=(10, 5))
stcl_acc.plot_tree(ax=ax, fontsize=20)
plt.show()

Tree with Balanced Classification Accuracy Objective¶
[25]:
stcl_balance = FlowOCT(
solver="gurobi",
depth=2,
obj_mode="balance",
_lambda=0,
verbose=False,
)
stcl_balance.fit(X, y)
predictions = stcl_balance.predict(X)
print(f"In-sample accuracy is {np.sum(predictions==y)/y.shape[0]}")
Set parameter Username
Academic license - for non-commercial use only - expires 2025-06-28
Set parameter TimeLimit to value 60
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 314 rows, 237 columns and 734 nonzeros
Model fingerprint: 0x3bc6df12
Variable types: 224 continuous, 13 integer (13 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [4e-02, 2e-01]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Found heuristic solution: objective -0.0000000
Presolve removed 269 rows and 203 columns
Presolve time: 0.01s
Presolved: 45 rows, 34 columns, 134 nonzeros
Found heuristic solution: objective 0.5000000
Variable types: 27 continuous, 7 integer (7 binary)
Root relaxation: objective 7.500000e-01, 31 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 0.75000 0 1 0.50000 0.75000 50.0% - 0s
H 0 0 0.5288462 0.75000 41.8% - 0s
H 0 0 0.6730769 0.75000 11.4% - 0s
0 0 0.67308 0 4 0.67308 0.67308 0.00% - 0s
Cutting planes:
MIR: 1
Flow cover: 1
Explored 1 nodes (36 simplex iterations) in 0.01 seconds (0.00 work units)
Thread count was 8 (of 8 available processors)
Solution count 3: 0.673077 0.5 -0
No other solutions better than 0.673077
Optimal solution found (tolerance 1.00e-04)
Best objective 6.730769230769e-01, best bound 6.730769230769e-01, gap 0.0000%
In-sample accuracy is 0.8
[26]:
fig, ax = plt.subplots(figsize=(10, 5))
stcl_balance.plot_tree(ax=ax, fontsize=20)
plt.show()

As we can see, when we maximize accuracy, i.e., when obj_mode = 'acc', the optimal tree is just a single node without branching, predicting the majority class for the whole dataset. But when we change the objective mode to balanced accuracy, we account for the minority class by sacrificing the overal accuracy.
Example 3: UCI Data Example¶
In this section, we fit a tree of depth 3 on a real world dataset called the `balance dataset <https://archive.ics.uci.edu/ml/datasets/Balance+Scale>`__ from the UCI Machine Learning repository.
[27]:
import pandas as pd
from sklearn.model_selection import train_test_split
from odtlearn.datasets import balance_scale_data
[28]:
# read data
data = balance_scale_data()
print(f"shape{data.shape}")
data.columns
shape(625, 21)
[28]:
Index(['V2.1', 'V2.2', 'V2.3', 'V2.4', 'V2.5', 'V3.1', 'V3.2', 'V3.3', 'V3.4',
'V3.5', 'V4.1', 'V4.2', 'V4.3', 'V4.4', 'V4.5', 'V5.1', 'V5.2', 'V5.3',
'V5.4', 'V5.5', 'target'],
dtype='object')
[29]:
y = data.pop("target")
X_train, X_test, y_train, y_test = train_test_split(
data, y, test_size=0.33, random_state=42
)
[30]:
stcl = BendersOCT(solver="gurobi", depth=3, time_limit=200, obj_mode="acc", verbose=True)
stcl.fit(X_train, y_train)
Set parameter Username
Academic license - for non-commercial use only - expires 2025-06-28
Set parameter TimeLimit to value 200
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter LazyConstraints to value 1
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 30 rows, 618 columns and 249 nonzeros
Model fingerprint: 0xaeff5467
Variable types: 463 continuous, 155 integer (155 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [1e+00, 1e+00]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Presolve removed 8 rows and 8 columns
Presolve time: 0.00s
Presolved: 22 rows, 610 columns, 233 nonzeros
Variable types: 463 continuous, 147 integer (147 binary)
Root relaxation presolved: 412 rows, 610 columns, 7100 nonzeros
Concurrent LP optimizer: primal simplex, dual simplex, and barrier
Showing barrier log only...
Root barrier log...
Ordering time: 0.00s
Barrier performed 0 iterations in 0.18 seconds (0.00 work units)
Barrier solve interrupted - model solved by another algorithm
Solved with dual simplex
Root relaxation: objective 4.180000e+02, 77 iterations, 0.01 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 418.00000 0 4 - 418.00000 - - 0s
H 0 0 269.0000000 418.00000 55.4% - 0s
0 0 418.00000 0 4 269.00000 418.00000 55.4% - 0s
0 2 413.60000 0 9 269.00000 413.60000 53.8% - 0s
H 308 294 272.0000000 413.60000 52.1% 75.5 1s
H 483 460 274.0000000 413.60000 50.9% 75.6 1s
* 533 475 54 290.0000000 413.60000 42.6% 73.6 1s
1143 887 cutoff 64 290.00000 412.40000 42.2% 78.6 5s
H 1310 970 291.0000000 412.40000 41.7% 75.5 5s
1556 1132 316.00000 35 26 291.00000 409.65561 40.8% 70.5 10s
1629 1180 371.73684 22 25 291.00000 403.03327 38.5% 67.3 15s
1797 1290 367.57918 36 10 291.00000 402.21668 38.2% 92.8 20s
H 2163 1398 293.0000000 400.54472 36.7% 92.9 21s
* 2375 1361 111 296.0000000 399.64465 35.0% 91.6 22s
H 3419 1561 299.0000000 398.14472 33.2% 86.5 24s
3861 1733 358.57143 67 20 299.00000 398.14472 33.2% 87.2 25s
H 4454 1024 312.0000000 398.14472 27.6% 85.7 25s
8785 2721 cutoff 62 312.00000 358.67679 15.0% 82.5 30s
16715 6109 313.50000 67 16 312.00000 338.60887 8.53% 69.7 35s
H17827 5595 314.0000000 338.16497 7.70% 67.8 35s
26793 9027 315.00000 77 8 314.00000 330.38947 5.22% 59.2 40s
H31789 9084 315.0000000 329.54167 4.62% 57.5 43s
33926 9710 318.00000 71 8 315.00000 328.75000 4.37% 56.7 45s
H35037 8771 316.0000000 328.02174 3.80% 56.5 45s
H36500 6760 318.0000000 327.50000 2.99% 56.0 46s
42743 6716 322.50000 59 12 318.00000 325.00000 2.20% 54.1 50s
54532 4635 cutoff 48 318.00000 321.00000 0.94% 50.5 55s
65931 1611 cutoff 74 318.00000 319.48148 0.47% 47.7 60s
Cutting planes:
MIR: 120
Flow cover: 193
Lazy constraints: 236
Explored 70775 nodes (3292092 simplex iterations) in 61.92 seconds (141.79 work units)
Thread count was 8 (of 8 available processors)
Solution count 10: 318 316 315 ... 290
Optimal solution found (tolerance 1.00e-04)
Best objective 3.180000000000e+02, best bound 3.180000000000e+02, gap 0.0000%
User-callback calls 150674, time in user-callback 1.85 sec
[30]:
BendersOCT(solver=gurobi,depth=3,time_limit=200,num_threads=None,verbose=True)
[31]:
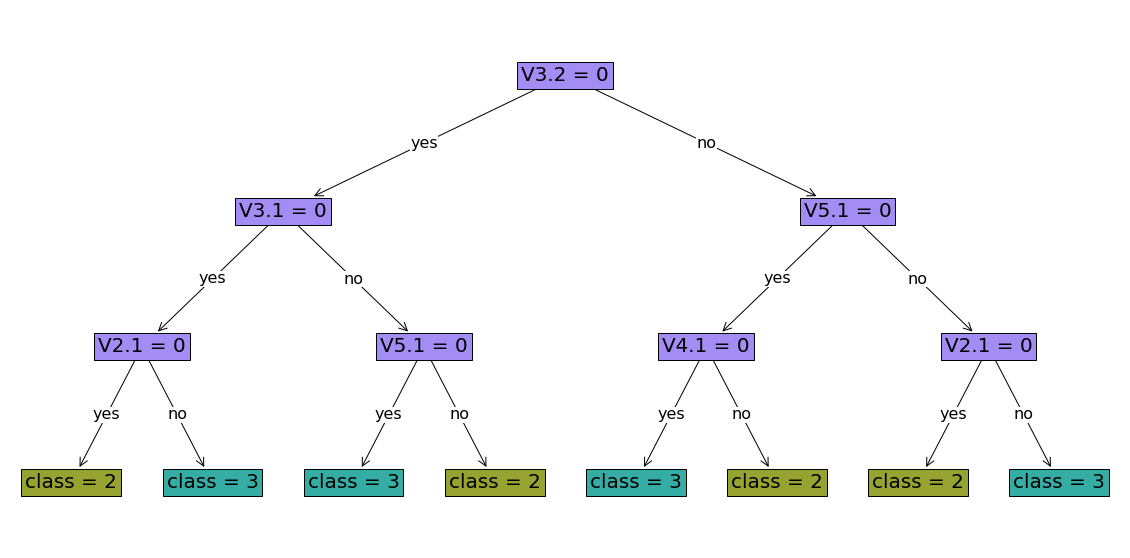
stcl.print_tree()
#########node 1
branch on V3.2
#########node 2
branch on V3.1
#########node 3
branch on V5.1
#########node 4
branch on V2.1
#########node 5
branch on V5.1
#########node 6
branch on V4.1
#########node 7
branch on V2.1
#########node 8
leaf 2
#########node 9
leaf 3
#########node 10
leaf 3
#########node 11
leaf 2
#########node 12
leaf 3
#########node 13
leaf 2
#########node 14
leaf 2
#########node 15
leaf 3
[32]:
fig, ax = plt.subplots(figsize=(20, 10))
stcl.plot_tree(ax=ax, fontsize=20, color_dict={"node": None, "leaves": []})
plt.show()
[33]:
test_pred = stcl.predict(X_test)
print('The out-of-sample accuracy is {}'.format(np.sum(test_pred==y_test)/y_test.shape[0]))
The out-of-sample accuracy is 0.6859903381642513
Example 4: User-defined Weights¶
In this example, we’ll demonstrate how to use user-defined weights with FlowOCT and BendersOCT. We’ll use a small binary classification dataset and show how user-defined weights can affect the learned tree.
First, let’s create our small binary classification dataset:
[34]:
np.random.seed(42)
X = np.random.randint(0, 2, size=(20, 5))
y = np.random.randint(0, 2, size=20)
print("Dataset shape:", X.shape)
print("Class distribution:", np.bincount(y))
Dataset shape: (20, 5)
Class distribution: [ 6 14]
Now, let’s create weights that heavily favor class 1:
[35]:
weights = np.ones_like(y)
weights[y == 1] = 10
print("Weight distribution:")
print("Class 0:", weights[y == 0].mean())
print("Class 1:", weights[y == 1].mean())
Weight distribution:
Class 0: 1.0
Class 1: 10.0
FlowOCT with User-defined Weights¶
Let’s fit a FlowOCT model with user-defined weights and compare it to a model without the accuracy objective:
[36]:
# FlowOCT without custom weights
flow_oct_default = FlowOCT(solver="gurobi", obj_mode="acc", depth=2, time_limit=10)
flow_oct_default.fit(X, y)
# FlowOCT with custom weights
flow_oct_custom = FlowOCT(solver="gurobi", obj_mode="weighted", depth=2, time_limit=10)
flow_oct_custom.fit(X, y, weights=weights)
print("Default FlowOCT predictions:", flow_oct_default.predict(X))
print("User-defined weights FlowOCT predictions:", flow_oct_custom.predict(X))
print("Default FlowOCT accuracy:", (flow_oct_default.predict(X) == y).mean())
print("User-defined weights FlowOCT accuracy:", (flow_oct_custom.predict(X) == y).mean())
print("User-defined weights FlowOCT weighted accuracy:", np.average(flow_oct_custom.predict(X) == y, weights=weights))
Set parameter Username
Academic license - for non-commercial use only - expires 2025-06-28
Set parameter TimeLimit to value 10
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 414 rows, 316 columns and 1153 nonzeros
Model fingerprint: 0x1ad65f5a
Variable types: 294 continuous, 22 integer (22 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [1e+00, 1e+00]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Found heuristic solution: objective -0.0000000
Presolve removed 205 rows and 186 columns
Presolve time: 0.00s
Presolved: 209 rows, 130 columns, 660 nonzeros
Found heuristic solution: objective 14.0000000
Variable types: 112 continuous, 18 integer (18 binary)
Root relaxation: objective 1.966667e+01, 166 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 19.66667 0 7 14.00000 19.66667 40.5% - 0s
H 0 0 16.0000000 19.66667 22.9% - 0s
H 0 0 17.0000000 19.00000 11.8% - 0s
0 0 18.50000 0 9 17.00000 18.50000 8.82% - 0s
Cutting planes:
Gomory: 13
MIR: 6
RLT: 20
Explored 1 nodes (198 simplex iterations) in 0.01 seconds (0.01 work units)
Thread count was 8 (of 8 available processors)
Solution count 4: 17 16 14 -0
Optimal solution found (tolerance 1.00e-04)
Best objective 1.700000000000e+01, best bound 1.700000000000e+01, gap 0.0000%
Set parameter Username
Academic license - for non-commercial use only - expires 2025-06-28
Set parameter TimeLimit to value 10
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 414 rows, 316 columns and 1153 nonzeros
Model fingerprint: 0xf6c20781
Variable types: 294 continuous, 22 integer (22 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [1e+00, 1e+01]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Found heuristic solution: objective -0.0000000
Presolve removed 205 rows and 186 columns
Presolve time: 0.00s
Presolved: 209 rows, 130 columns, 660 nonzeros
Found heuristic solution: objective 140.0000000
Variable types: 112 continuous, 18 integer (18 binary)
Root relaxation: objective 1.456667e+02, 173 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 145.66667 0 7 140.00000 145.66667 4.05% - 0s
H 0 0 143.0000000 144.66667 1.17% - 0s
0 0 144.00000 0 11 143.00000 144.00000 0.70% - 0s
0 0 143.00000 0 6 143.00000 143.00000 0.00% - 0s
Cutting planes:
Gomory: 1
MIR: 1
RLT: 7
Explored 1 nodes (233 simplex iterations) in 0.01 seconds (0.01 work units)
Thread count was 8 (of 8 available processors)
Solution count 3: 143 140 -0
Optimal solution found (tolerance 1.00e-04)
Best objective 1.430000000000e+02, best bound 1.430000000000e+02, gap 0.0000%
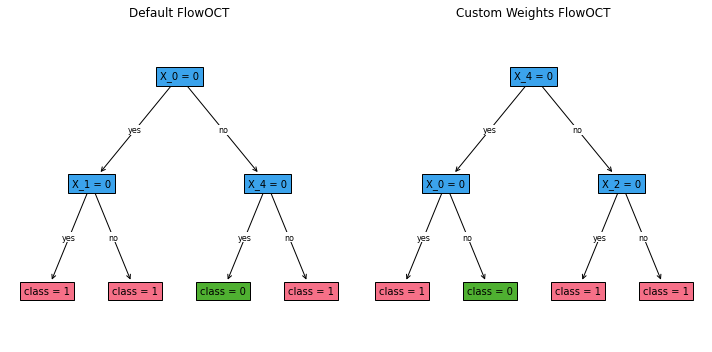
Default FlowOCT predictions: [1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 0]
Custom weights FlowOCT predictions: [1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 0]
Default FlowOCT accuracy: 0.85
Custom weights FlowOCT accuracy: 0.85
Custom weights FlowOCT weighted accuracy: 0.9794520547945206
Let’s visualize both trees:
[37]:
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
flow_oct_default.plot_tree(ax=ax1, fontsize=10)
ax1.set_title("Default FlowOCT")
flow_oct_custom.plot_tree(ax=ax2, fontsize=10)
ax2.set_title("User-defined Weights FlowOCT")
plt.tight_layout()
plt.show()
BendersOCT with User-defined Weights¶
Now let’s do the same with BendersOCT:
[38]:
# BendersOCT without custom weights
benders_oct_default = BendersOCT(solver="gurobi", obj_mode="acc", depth=2, time_limit=10)
benders_oct_default.fit(X, y)
# BendersOCT with custom weights
benders_oct_custom = BendersOCT(solver="gurobi", obj_mode="weighted", depth=2, time_limit=10, verbose=False)
benders_oct_custom.fit(X, y, weights=weights)
print("Default BendersOCT predictions:", benders_oct_default.predict(X))
print("User-defined weights BendersOCT predictions:", benders_oct_custom.predict(X))
print("Default BendersOCT accuracy:", (benders_oct_default.predict(X) == y).mean())
print("User-defined weights BendersOCT accuracy:", (benders_oct_custom.predict(X) == y).mean())
print("User-defined weights BendersOCT weighted accuracy:", np.average(benders_oct_custom.predict(X) == y, weights=weights))
Set parameter Username
Academic license - for non-commercial use only - expires 2025-06-28
Set parameter TimeLimit to value 10
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter LazyConstraints to value 1
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 14 rows, 56 columns and 53 nonzeros
Model fingerprint: 0x28902962
Variable types: 34 continuous, 22 integer (22 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [1e+00, 1e+00]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Presolve removed 4 rows and 4 columns
Presolve time: 0.00s
Presolved: 10 rows, 52 columns, 45 nonzeros
Variable types: 34 continuous, 18 integer (18 binary)
Root relaxation presolved: 22 rows, 50 columns, 140 nonzeros
Root relaxation: objective 2.000000e+01, 2 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 20.00000 0 - - 20.00000 - - 0s
0 0 20.00000 0 - - 20.00000 - - 0s
0 0 20.00000 0 - - 20.00000 - - 0s
0 0 20.00000 0 7 - 20.00000 - - 0s
H 0 0 14.0000000 20.00000 42.9% - 0s
H 0 0 16.0000000 20.00000 25.0% - 0s
0 0 19.50000 0 2 16.00000 19.50000 21.9% - 0s
0 0 19.26563 0 9 16.00000 19.26563 20.4% - 0s
H 0 0 17.0000000 19.26563 13.3% - 0s
0 0 19.00000 0 8 17.00000 19.00000 11.8% - 0s
0 0 18.96429 0 9 17.00000 18.96429 11.6% - 0s
0 0 18.95833 0 9 17.00000 18.95833 11.5% - 0s
0 0 18.85000 0 9 17.00000 18.85000 10.9% - 0s
0 0 18.85000 0 9 17.00000 18.85000 10.9% - 0s
0 0 18.76563 0 11 17.00000 18.76563 10.4% - 0s
0 0 18.74194 0 10 17.00000 18.74194 10.2% - 0s
0 0 18.73913 0 9 17.00000 18.73913 10.2% - 0s
0 0 18.59091 0 9 17.00000 18.59091 9.36% - 0s
0 0 18.50000 0 9 17.00000 18.50000 8.82% - 0s
0 0 18.50000 0 9 17.00000 18.50000 8.82% - 0s
0 0 18.37500 0 8 17.00000 18.37500 8.09% - 0s
0 0 18.33333 0 8 17.00000 18.33333 7.84% - 0s
0 0 18.33333 0 9 17.00000 18.33333 7.84% - 0s
0 0 18.31250 0 7 17.00000 18.31250 7.72% - 0s
0 0 18.30000 0 7 17.00000 18.30000 7.65% - 0s
0 0 18.16667 0 7 17.00000 18.16667 6.86% - 0s
0 0 18.14706 0 8 17.00000 18.14706 6.75% - 0s
0 0 18.09524 0 10 17.00000 18.09524 6.44% - 0s
0 0 18.07059 0 10 17.00000 18.07059 6.30% - 0s
0 0 18.03478 0 10 17.00000 18.03478 6.09% - 0s
0 0 18.01765 0 11 17.00000 18.01765 5.99% - 0s
0 0 18.01333 0 11 17.00000 18.01333 5.96% - 0s
0 0 18.00532 0 12 17.00000 18.00532 5.91% - 0s
0 0 18.00463 0 12 17.00000 18.00463 5.91% - 0s
0 0 17.95833 0 9 17.00000 17.95833 5.64% - 0s
0 0 17.91304 0 8 17.00000 17.91304 5.37% - 0s
0 0 17.91304 0 8 17.00000 17.91304 5.37% - 0s
0 0 17.90909 0 8 17.00000 17.90909 5.35% - 0s
0 0 17.90909 0 11 17.00000 17.90909 5.35% - 0s
0 0 17.89873 0 11 17.00000 17.89873 5.29% - 0s
0 0 17.89873 0 10 17.00000 17.89873 5.29% - 0s
0 2 17.89873 0 10 17.00000 17.89873 5.29% - 0s
Cutting planes:
Gomory: 1
MIR: 11
Flow cover: 5
Lazy constraints: 46
Explored 16 nodes (312 simplex iterations) in 0.05 seconds (0.02 work units)
Thread count was 8 (of 8 available processors)
Solution count 3: 17 16 14
Optimal solution found (tolerance 1.00e-04)
Best objective 1.700000000000e+01, best bound 1.700000000000e+01, gap 0.0000%
User-callback calls 366, time in user-callback 0.02 sec
Set parameter Username
Academic license - for non-commercial use only - expires 2025-06-28
Set parameter TimeLimit to value 10
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter LazyConstraints to value 1
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 14 rows, 56 columns and 53 nonzeros
Model fingerprint: 0x75b5cba0
Variable types: 34 continuous, 22 integer (22 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [1e+00, 1e+01]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Presolve removed 4 rows and 4 columns
Presolve time: 0.00s
Presolved: 10 rows, 52 columns, 45 nonzeros
Variable types: 34 continuous, 18 integer (18 binary)
Root relaxation presolved: 22 rows, 50 columns, 140 nonzeros
Root relaxation: objective 1.460000e+02, 2 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 146.00000 0 - - 146.00000 - - 0s
0 0 146.00000 0 - - 146.00000 - - 0s
0 0 146.00000 0 - - 146.00000 - - 0s
0 0 146.00000 0 7 - 146.00000 - - 0s
H 0 0 140.0000000 146.00000 4.29% - 0s
0 0 145.50000 0 4 140.00000 145.50000 3.93% - 0s
0 0 145.37500 0 7 140.00000 145.37500 3.84% - 0s
H 0 0 143.0000000 145.37500 1.66% - 0s
0 0 144.88542 0 10 143.00000 144.88542 1.32% - 0s
0 0 144.88194 0 10 143.00000 144.88194 1.32% - 0s
0 0 144.33333 0 7 143.00000 144.33333 0.93% - 0s
0 0 144.30000 0 7 143.00000 144.30000 0.91% - 0s
0 0 144.16667 0 7 143.00000 144.16667 0.82% - 0s
0 0 144.12500 0 9 143.00000 144.12500 0.79% - 0s
0 0 144.12500 0 9 143.00000 144.12500 0.79% - 0s
0 0 144.08333 0 11 143.00000 144.08333 0.76% - 0s
0 0 144.08036 0 11 143.00000 144.08036 0.76% - 0s
0 0 144.08036 0 11 143.00000 144.08036 0.76% - 0s
0 0 144.02737 0 10 143.00000 144.02737 0.72% - 0s
0 0 144.02737 0 11 143.00000 144.02737 0.72% - 0s
0 0 144.02632 0 11 143.00000 144.02632 0.72% - 0s
0 0 144.02632 0 10 143.00000 144.02632 0.72% - 0s
0 2 144.02632 0 9 143.00000 144.02632 0.72% - 0s
Cutting planes:
Gomory: 1
MIR: 3
Flow cover: 9
Lazy constraints: 47
Explored 14 nodes (157 simplex iterations) in 0.03 seconds (0.01 work units)
Thread count was 8 (of 8 available processors)
Solution count 2: 143 140
Optimal solution found (tolerance 1.00e-04)
Best objective 1.430000000000e+02, best bound 1.430000000000e+02, gap 0.0000%
Default BendersOCT predictions: [1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 0]
Custom weights BendersOCT predictions: [1 1 1 1 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 0]
Default BendersOCT accuracy: 0.85
Custom weights BendersOCT accuracy: 0.85
User-callback calls 283, time in user-callback 0.01 sec
Custom weights BendersOCT weighted accuracy: 0.9794520547945206
[39]:
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 5))
benders_oct_default.plot_tree(ax=ax1, fontsize=10)
ax1.set_title("Default BendersOCT")
benders_oct_custom.plot_tree(ax=ax2, fontsize=10)
ax2.set_title("User-defined Weights BendersOCT")
plt.tight_layout()
plt.show()
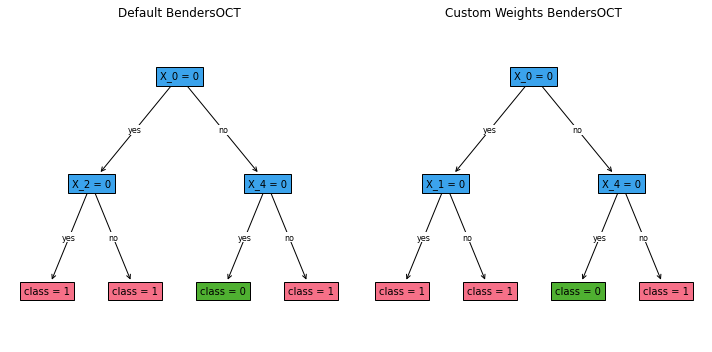
In this example, we’ve demonstrated how to use user-defined weights with both FlowOCT and BendersOCT. By setting obj_mode="weighted" and providing weights during the fit method call, we can influence the importance of different samples in the training process. The user-defined weights in this example heavily favor class 1, which may result in trees that are more likely to predict class 1, potentially at the cost of overall accuracy. However, this can be useful in scenarios where
misclassifying one class is more costly than misclassifying the other, or when dealing with imbalanced datasets. Note that the actual results may vary due to the random nature of the dataset and the optimization process. You may want to run the code multiple times or with different random seeds to get a better understanding of the effects of user-defined weights.
References¶
Dua, D. and Graff, C. (2019). UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science.
Aghaei, S., Gómez, A., & Vayanos, P. (2021). Strong optimal classification trees. arXiv preprint arXiv:2103.15965. https://arxiv.org/abs/2103.15965.