RobustOCT Examples¶
Example 1: Synthetic Data Without Specified Shifts¶
If costs and/or budget is not specified, then we will produce the same result as an optimal strong classification tree.
As an example, say that we are given this training set:
[27]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from odtlearn.robust_oct import RobustOCT
"""
X2
| |
| |
1 + + | -
| |
|---------------|-------------
| |
0 - - - - | + + +
| - - - |
|______0________|_______1_______X1
"""
X = np.array(
[
[0, 0],
[0, 0],
[0, 0],
[0, 0],
[0, 0],
[0, 0],
[0, 0],
[1, 0],
[1, 0],
[1, 0],
[1, 1],
[0, 1],
[0, 1],
]
)
X = pd.DataFrame(X, columns=["X1", "X2"])
y = np.array([0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1])
If either costs or budget is not specified, the optimal classification tree will be produced (i.e., a tree that does not account for distribution shifts).
[28]:
from odtlearn.robust_oct import RobustOCT
robust_classifier = RobustOCT(
solver="gurobi",
depth = 2,
time_limit = 100,
)
robust_classifier.fit(X, y)
predictions = robust_classifier.predict(X)
Set parameter Username
Academic license - for non-commercial use only - expires 2024-06-27
Set parameter TimeLimit to value 100
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter LazyConstraints to value 1
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 7 rows, 33 columns and 20 nonzeros
Model fingerprint: 0x78ba3dea
Variable types: 13 continuous, 20 integer (20 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [2e-01, 1e+00]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Presolve removed 4 rows and 4 columns
Presolve time: 0.01s
Presolved: 3 rows, 29 columns, 12 nonzeros
Variable types: 13 continuous, 16 integer (16 binary)
Root relaxation presolved: 12 rows, 29 columns, 65 nonzeros
Root relaxation: objective 1.300000e+01, 5 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 13.00000 0 - - 13.00000 - - 0s
0 0 12.75000 0 - - 12.75000 - - 0s
0 0 12.75000 0 - - 12.75000 - - 0s
0 0 12.50000 0 6 - 12.50000 - - 0s
H 0 0 7.2500000 12.50000 72.4% - 0s
H 0 0 10.5000000 12.50000 19.0% - 0s
0 0 12.38889 0 5 10.50000 12.38889 18.0% - 0s
0 0 12.25000 0 7 10.50000 12.25000 16.7% - 0s
0 0 12.25000 0 - 10.50000 12.25000 16.7% - 0s
* 0 0 0 12.2500000 12.25000 0.00% - 0s
Cutting planes:
Gomory: 1
MIR: 3
Lazy constraints: 44
Explored 1 nodes (32 simplex iterations) in 0.06 seconds (0.00 work units)
Thread count was 8 (of 8 available processors)
Solution count 3: 12.25 10.5 7.25
Optimal solution found (tolerance 1.00e-04)
Best objective 1.225000000000e+01, best bound 1.225000000000e+01, gap 0.0000%
User-callback calls 170, time in user-callback 0.02 sec
[29]:
robust_classifier.print_tree()
#########node 1
Feature: X2 , Cutoff: 0
#########node 2
Feature: X1 , Cutoff: 0
#########node 3
Feature: X1 , Cutoff: 0
#########node 4
leaf 0
#########node 5
leaf 1
#########node 6
leaf 1
#########node 7
leaf 0
[30]:
fig, ax = plt.subplots(figsize=(10, 5))
robust_classifier.plot_tree()
plt.show()
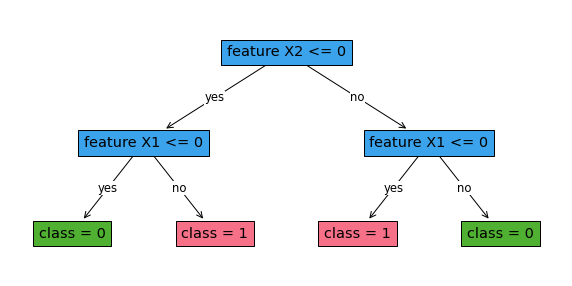
Example 2: synthetic data with specified shifts¶
We take the same synthetic data from Example 1, but now add distribution shifts with the following schema: - For 5 samples at ![[0,0]](../_images/math/ebf9e680273a1d5e209eb0e2a4b13a19620a103b.png)
, pay a cost of 1 to perturb 
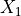and get ![[1,0]](../_images/math/89373012d8df0f30839ffc7ef5cb142d7a990cb0.png)
- For the 1 sample at ![[1,1]](../_images/math/6cf1b5020649f69c2f029417055708155cca1ece.png)
, pay a cost of 1 to perturb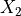 
to get - All other perturbations are not allowed
First, define these costs, which have the same shape and features as your input sample.
[31]:
# Note: 10 is a proxy for infinite cost, as it is over the allowed budgets we will specify
costs = np.array([[1,10],[1,10],[1,10],[1,10],[1,10],[10,10],[10,10],
[10,10],[10,10],[10,10],
[10,1],
[10,10],[10,10]])
costs = pd.DataFrame(costs, columns=['X1', 'X2'])
When the budget is 2 (corresponding to the variable ε), we don’t see a change in the tree from Example 1 since for this dataset, the budget is small and thus the level of robustness is small.
[32]:
# Same data as Example 1
X = np.array(
[
[0, 0],
[0, 0],
[0, 0],
[0, 0],
[0, 0],
[0, 0],
[0, 0],
[1, 0],
[1, 0],
[1, 0],
[1, 1],
[0, 1],
[0, 1],
]
)
X = pd.DataFrame(X, columns=["X1", "X2"])
y = np.array([0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1])
[33]:
robust_classifier = RobustOCT(
solver="gurobi",
depth=2,
time_limit=100
)
robust_classifier.fit(X, y, costs=costs, budget=2)
predictions = robust_classifier.predict(X)
Set parameter Username
Academic license - for non-commercial use only - expires 2024-06-27
Set parameter TimeLimit to value 100
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter LazyConstraints to value 1
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 7 rows, 33 columns and 20 nonzeros
Model fingerprint: 0x78ba3dea
Variable types: 13 continuous, 20 integer (20 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [2e-01, 1e+00]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Presolve removed 4 rows and 4 columns
Presolve time: 0.00s
Presolved: 3 rows, 29 columns, 12 nonzeros
Variable types: 13 continuous, 16 integer (16 binary)
Root relaxation presolved: 12 rows, 29 columns, 65 nonzeros
Root relaxation: objective 1.300000e+01, 5 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 13.00000 0 - - 13.00000 - - 0s
0 0 12.75000 0 - - 12.75000 - - 0s
0 0 12.75000 0 - - 12.75000 - - 0s
0 0 12.50000 0 6 - 12.50000 - - 0s
H 0 0 7.2500000 12.50000 72.4% - 0s
H 0 0 8.5000000 12.50000 47.1% - 0s
0 0 12.38889 0 5 8.50000 12.38889 45.8% - 0s
0 0 12.27513 0 11 8.50000 12.27513 44.4% - 0s
0 0 12.25000 0 9 8.50000 12.25000 44.1% - 0s
H 0 0 9.2500000 12.25000 32.4% - 0s
H 0 0 9.5000000 12.25000 28.9% - 0s
0 0 12.25000 0 6 9.50000 12.25000 28.9% - 0s
0 0 12.25000 0 - 9.50000 12.25000 28.9% - 0s
0 0 12.23554 0 13 9.50000 12.23554 28.8% - 0s
0 0 12.22893 0 11 9.50000 12.22893 28.7% - 0s
H 0 0 10.2500000 12.22893 19.3% - 0s
0 0 12.21106 0 11 10.25000 12.21106 19.1% - 0s
0 0 12.19909 0 11 10.25000 12.19909 19.0% - 0s
0 0 12.19909 0 11 10.25000 12.19909 19.0% - 0s
0 0 12.19909 0 11 10.25000 12.19909 19.0% - 0s
0 2 12.19909 0 11 10.25000 12.19909 19.0% - 0s
Cutting planes:
MIR: 5
Lazy constraints: 61
Explored 21 nodes (130 simplex iterations) in 0.05 seconds (0.01 work units)
Thread count was 8 (of 8 available processors)
Solution count 5: 10.25 9.5 9.25 ... 7.25
Optimal solution found (tolerance 1.00e-04)
Best objective 1.025000000000e+01, best bound 1.025000000000e+01, gap 0.0000%
User-callback calls 257, time in user-callback 0.03 sec
[34]:
robust_classifier.print_tree()
#########node 1
Feature: X2 , Cutoff: 0
#########node 2
Feature: X1 , Cutoff: 0
#########node 3
Feature: X1 , Cutoff: 0
#########node 4
leaf 0
#########node 5
leaf 1
#########node 6
leaf 1
#########node 7
leaf 0
[35]:
fig, ax = plt.subplots(figsize=(10, 5))
robust_classifier.plot_tree()
plt.show()
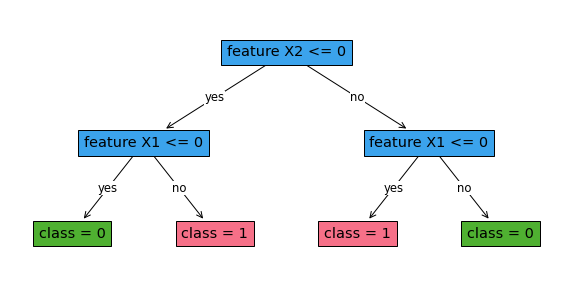
But when the budget is increased to 5 (adding more robustness), we see a change in the tree.
[36]:
robust_classifier = RobustOCT(
solver="gurobi",
depth=2,
time_limit=100
)
robust_classifier.fit(X, y, costs=costs, budget=5)
predictions = robust_classifier.predict(X)
Set parameter Username
Academic license - for non-commercial use only - expires 2024-06-27
Set parameter TimeLimit to value 100
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter LazyConstraints to value 1
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 7 rows, 33 columns and 20 nonzeros
Model fingerprint: 0x78ba3dea
Variable types: 13 continuous, 20 integer (20 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [2e-01, 1e+00]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Presolve removed 4 rows and 4 columns
Presolve time: 0.00s
Presolved: 3 rows, 29 columns, 12 nonzeros
Variable types: 13 continuous, 16 integer (16 binary)
Root relaxation presolved: 12 rows, 29 columns, 65 nonzeros
Root relaxation: objective 1.300000e+01, 5 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 13.00000 0 - - 13.00000 - - 0s
0 0 12.75000 0 - - 12.75000 - - 0s
0 0 12.75000 0 - - 12.75000 - - 0s
0 0 12.50000 0 6 - 12.50000 - - 0s
H 0 0 7.2500000 12.50000 72.4% - 0s
H 0 0 8.0000000 12.50000 56.2% - 0s
0 0 12.38889 0 5 8.00000 12.38889 54.9% - 0s
0 0 12.25000 0 9 8.00000 12.25000 53.1% - 0s
0 0 12.25000 0 6 8.00000 12.25000 53.1% - 0s
0 0 12.25000 0 - 8.00000 12.25000 53.1% - 0s
0 0 12.25000 0 7 8.00000 12.25000 53.1% - 0s
0 0 12.25000 0 7 8.00000 12.25000 53.1% - 0s
0 2 12.25000 0 7 8.00000 12.25000 53.1% - 0s
* 10 5 3 9.5000000 11.25000 18.4% 6.2 0s
Cutting planes:
MIR: 7
Lazy constraints: 69
Explored 24 nodes (153 simplex iterations) in 0.04 seconds (0.00 work units)
Thread count was 8 (of 8 available processors)
Solution count 3: 9.5 8 7.25
Optimal solution found (tolerance 1.00e-04)
Best objective 9.500000000000e+00, best bound 9.500000000000e+00, gap 0.0000%
User-callback calls 236, time in user-callback 0.02 sec
[37]:
robust_classifier.print_tree()
#########node 1
Feature: X2 , Cutoff: 0
#########node 2
leaf 0
#########node 3
Feature: X1 , Cutoff: 0
#########node 4
pruned
#########node 5
pruned
#########node 6
leaf 1
#########node 7
leaf 0
[38]:
fig, ax = plt.subplots(figsize=(10, 5))
robust_classifier.plot_tree()
plt.show()
Example 3: UCI data example¶
Here, we’ll see the benefits of using robust optimization by perturbing the test set. We will use the MONK’s Problems dataset from the UCI Machine Learning Repository.
[39]:
from sklearn.model_selection import train_test_split
from odtlearn.datasets import robust_example
Fetch data and split to train and test
[40]:
"""Fetch data and split to train and test"""
data, y = robust_example()
X_train, X_test, y_train, y_test = train_test_split(
data, y, test_size=0.25, random_state=2
)
For sake of comparison, train a classification tree that does not consider the scenario where there is a distribution shift:
[41]:
"""Train a non-robust tree for comparison"""
from odtlearn.robust_oct import RobustOCT
# If you define no uncertainty, you get an optimal tree without regularization that maximizes accuracy
non_robust_classifier = RobustOCT(solver="gurobi", depth=2, time_limit=300)
non_robust_classifier.fit(X_train, y_train)
Set parameter Username
Academic license - for non-commercial use only - expires 2024-06-27
Set parameter TimeLimit to value 300
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter LazyConstraints to value 1
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 7 rows, 173 columns and 47 nonzeros
Model fingerprint: 0xafd32360
Variable types: 126 continuous, 47 integer (47 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [2e-01, 1e+00]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Presolve removed 4 rows and 4 columns
Presolve time: 0.00s
Presolved: 3 rows, 169 columns, 39 nonzeros
Variable types: 126 continuous, 43 integer (43 binary)
Root relaxation presolved: 82 rows, 169 columns, 1072 nonzeros
Root relaxation: objective 1.260000e+02, 5 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 126.00000 0 - - 126.00000 - - 0s
0 0 125.75000 0 - - 125.75000 - - 0s
0 0 125.75000 0 7 - 125.75000 - - 0s
H 0 0 77.2500000 125.75000 62.8% - 0s
H 0 0 78.0000000 125.75000 61.2% - 0s
0 0 125.55000 0 13 78.00000 125.55000 61.0% - 0s
0 0 125.54167 0 14 78.00000 125.54167 61.0% - 0s
0 2 125.53640 0 23 78.00000 125.53640 60.9% - 0s
* 206 151 16 81.5000000 124.91667 53.3% 30.9 0s
* 934 451 8 82.2500000 112.02237 36.2% 26.9 1s
* 2715 519 15 83.2500000 95.50000 14.7% 21.4 1s
Cutting planes:
MIR: 6
Lazy constraints: 994
Explored 3627 nodes (70039 simplex iterations) in 1.70 seconds (1.53 work units)
Thread count was 8 (of 8 available processors)
Solution count 5: 83.25 82.25 81.5 ... 77.25
Optimal solution found (tolerance 1.00e-04)
Best objective 8.325000000000e+01, best bound 8.325000000000e+01, gap 0.0000%
User-callback calls 7707, time in user-callback 0.94 sec
[41]:
RobustOCT(solver=gurobi,depth=2,time_limit=300,num_threads=None,verbose=False)
[42]:
non_robust_classifier.print_tree()
#########node 1
Feature: Feat5 , Cutoff: 1
#########node 2
Feature: Feat3 , Cutoff: 2
#########node 3
Feature: Feat2 , Cutoff: 1
#########node 4
leaf 0
#########node 5
leaf 1
#########node 6
leaf 1
#########node 7
leaf 0
[43]:
fig, ax = plt.subplots(figsize=(10, 5))
non_robust_classifier.plot_tree()
plt.show()
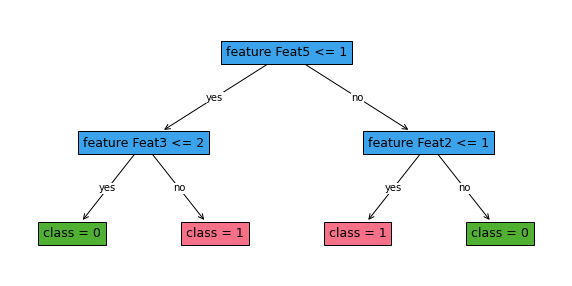
Train a robust tree. First, define the uncertainty. Here, we will generate a probability of certainty for each feature randomly (in practice, you would need to use some guess from domain knowledge). For simplicity, we will not change this probability by data sample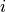 
. We also define 
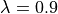, which in practice must be tuned.
[44]:
"""Generate q_f values for each feature (i.e. probability of certainty for feature f)"""
np.random.seed(42)
q_f = np.random.normal(loc=0.9, scale=0.1, size=len(X_train.columns))
# Snap q_f to range [0,1]
q_f[q_f <= 0] = np.nextafter(np.float32(0), np.float32(1))
q_f[q_f > 1] = 1.0
q_f
[44]:
array([0.94967142, 0.88617357, 0.96476885, 1. , 0.87658466,
0.8765863 ])
Calibrate the costs and budget parameters for the fit function.
[45]:
"""Define budget of uncertainty"""
from math import log
l = 0.9 # Lambda value between 0 and 1
budget = -1 * X_train.shape[0] * log(l)
budget
[45]:
13.275424972886112
[46]:
"""Based on q_f values, create costs of uncertainty"""
from copy import deepcopy
costs = deepcopy(X_train)
costs = costs.astype("float")
for f in range(len(q_f)):
if q_f[f] == 1:
costs[costs.columns[f]] = budget + 1 # no uncertainty = "infinite" cost
else:
costs[costs.columns[f]] = -1 * log(1 - q_f[f])
costs
[46]:
| Feat0 | Feat1 | Feat2 | Feat3 | Feat4 | Feat5 | |
|---|---|---|---|---|---|---|
| 0 | 2.989182 | 2.173081 | 3.345825 | 14.275425 | 2.0922 | 2.092213 |
| 1 | 2.989182 | 2.173081 | 3.345825 | 14.275425 | 2.0922 | 2.092213 |
| 2 | 2.989182 | 2.173081 | 3.345825 | 14.275425 | 2.0922 | 2.092213 |
| 3 | 2.989182 | 2.173081 | 3.345825 | 14.275425 | 2.0922 | 2.092213 |
| 4 | 2.989182 | 2.173081 | 3.345825 | 14.275425 | 2.0922 | 2.092213 |
| ... | ... | ... | ... | ... | ... | ... |
| 121 | 2.989182 | 2.173081 | 3.345825 | 14.275425 | 2.0922 | 2.092213 |
| 122 | 2.989182 | 2.173081 | 3.345825 | 14.275425 | 2.0922 | 2.092213 |
| 123 | 2.989182 | 2.173081 | 3.345825 | 14.275425 | 2.0922 | 2.092213 |
| 124 | 2.989182 | 2.173081 | 3.345825 | 14.275425 | 2.0922 | 2.092213 |
| 125 | 2.989182 | 2.173081 | 3.345825 | 14.275425 | 2.0922 | 2.092213 |
126 rows × 6 columns
Train the robust tree using the costs and budget.
[47]:
robust_classifier = RobustOCT(
solver="gurobi",
depth=2,
time_limit=200,
)
robust_classifier.fit(X_train, y_train, costs=costs, budget=budget)
Set parameter Username
Academic license - for non-commercial use only - expires 2024-06-27
Set parameter TimeLimit to value 200
Set parameter NodeLimit to value 1073741824
Set parameter SolutionLimit to value 1073741824
Set parameter LazyConstraints to value 1
Set parameter IntFeasTol to value 1e-06
Set parameter Method to value 3
Gurobi Optimizer version 10.0.2 build v10.0.2rc0 (mac64[arm])
CPU model: Apple M1 Pro
Thread count: 8 physical cores, 8 logical processors, using up to 8 threads
Optimize a model with 7 rows, 173 columns and 47 nonzeros
Model fingerprint: 0xafd32360
Variable types: 126 continuous, 47 integer (47 binary)
Coefficient statistics:
Matrix range [1e+00, 1e+00]
Objective range [2e-01, 1e+00]
Bounds range [1e+00, 1e+00]
RHS range [1e+00, 1e+00]
Presolve removed 4 rows and 4 columns
Presolve time: 0.00s
Presolved: 3 rows, 169 columns, 39 nonzeros
Variable types: 126 continuous, 43 integer (43 binary)
Root relaxation presolved: 82 rows, 169 columns, 1072 nonzeros
Root relaxation: objective 1.260000e+02, 5 iterations, 0.00 seconds (0.00 work units)
Nodes | Current Node | Objective Bounds | Work
Expl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time
0 0 126.00000 0 - - 126.00000 - - 0s
0 0 125.75000 0 - - 125.75000 - - 0s
0 0 125.75000 0 7 - 125.75000 - - 0s
H 0 0 77.2500000 125.75000 62.8% - 0s
H 0 0 78.0000000 125.75000 61.2% - 0s
0 0 125.55000 0 13 78.00000 125.55000 61.0% - 0s
0 0 125.54167 0 14 78.00000 125.54167 61.0% - 0s
0 2 125.53640 0 23 78.00000 125.53640 60.9% - 0s
* 472 333 14 78.5000000 122.24074 55.7% 29.0 1s
* 2519 887 14 79.5000000 99.00000 24.5% 20.5 3s
3648 758 85.00000 20 2 79.50000 90.91667 14.4% 19.2 5s
Cutting planes:
MIR: 6
Lazy constraints: 1319
Explored 5135 nodes (84698 simplex iterations) in 8.19 seconds (3.26 work units)
Thread count was 8 (of 8 available processors)
Solution count 4: 79.5 78.5 78 77.25
Optimal solution found (tolerance 1.00e-04)
Best objective 7.950000000000e+01, best bound 7.950000000000e+01, gap 0.0000%
User-callback calls 11149, time in user-callback 6.77 sec
[47]:
RobustOCT(solver=gurobi,depth=2,time_limit=200,num_threads=None,verbose=False)
[48]:
robust_classifier.print_tree()
#########node 1
Feature: Feat3 , Cutoff: 2
#########node 2
leaf 0
#########node 3
Feature: Feat2 , Cutoff: 1
#########node 4
pruned
#########node 5
pruned
#########node 6
leaf 1
#########node 7
leaf 0
[49]:
fig, ax = plt.subplots(figsize=(10, 5))
robust_classifier.plot_tree()
plt.show()
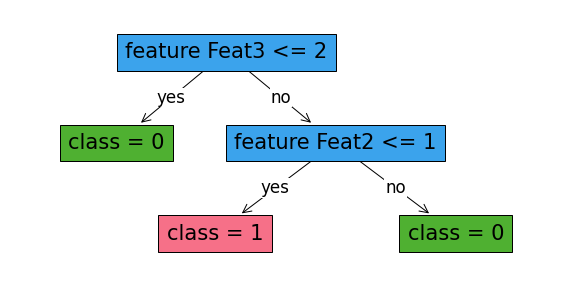
[50]:
from sklearn.metrics import accuracy_score
print(
"Non-robust training accuracy: ",
accuracy_score(y_train, non_robust_classifier.predict(X_train)),
)
print(
"Robust training accuracy: ",
accuracy_score(y_train, robust_classifier.predict(X_train)),
)
print(
"Non-robust test accuracy: ",
accuracy_score(y_test, non_robust_classifier.predict(X_test)),
)
print(
"Robust test accuracy: ",
accuracy_score(y_test, robust_classifier.predict(X_test)),
)
Non-robust training accuracy: 0.6666666666666666
Robust training accuracy: 0.6587301587301587
Non-robust test accuracy: 0.5813953488372093
Robust test accuracy: 0.5581395348837209
To measure the performance of the trained models, perturb the test data based off of our known certainties of each feature (to simulate a distribtion shift), and then see how well each tree performs against the perturbed data
[51]:
def perturb(data, q_f, seed):
"""Perturb X given q_f based off of the symmetric geometric distribution"""
new_data = deepcopy(data)
np.random.seed(seed)
# Perturbation of features
for f in range(len(new_data.columns)):
perturbations = np.random.geometric(q_f[f], size=new_data.shape[0])
perturbations = perturbations - 1 # Support should be 0,1,2,...
signs = (2 * np.random.binomial(1, 0.5, size=new_data.shape[0])) - 1
perturbations = perturbations * signs
new_data[new_data.columns[f]] = new_data[new_data.columns[f]] + perturbations
return new_data
"""Obtain 1000 different perturbed test sets, and record accuracies"""
non_robust_acc = []
robust_acc = []
for s in range(1, 1001):
X_test_perturbed = perturb(X_test, q_f, s)
non_robust_pred = non_robust_classifier.predict(X_test_perturbed)
robust_pred = robust_classifier.predict(X_test_perturbed)
non_robust_acc += [accuracy_score(y_test, non_robust_pred)]
robust_acc += [accuracy_score(y_test, robust_pred)]
[52]:
print("Worst-case accuracy (Non-Robust Tree): ", min(non_robust_acc))
print("Worst-case accuracy (Robust Tree): ", min(robust_acc))
print(
"Average accuracy (Non-Robust Tree): ", sum(non_robust_acc) / len(non_robust_acc)
)
print("Average accuracy (Robust Tree): ", sum(robust_acc) / len(robust_acc))
Worst-case accuracy (Non-Robust Tree): 0.4418604651162791
Worst-case accuracy (Robust Tree): 0.5116279069767442
Average accuracy (Non-Robust Tree): 0.5660930232558059
Average accuracy (Robust Tree): 0.5584186046511533
References¶
Justin, N., Aghaei, S., Gómez, A., & Vayanos, P. (2022). Optimal robust classification trees. The AAAI-2022 Workshop on Adversarial Machine Learning and Beyond. https://openreview.net/pdf?id=HbasA9ysA3
Dua, D. and Graff, C. (2019). UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science.